
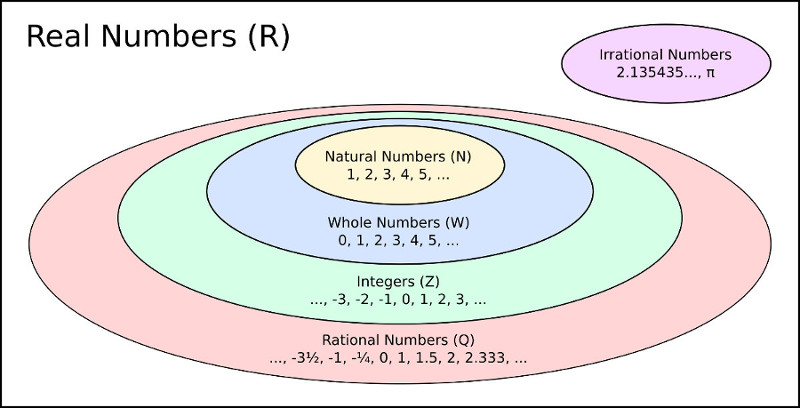
They are not called "Real" because they show the value of something real. That is the actual answer! Real does not mean they are in the real world They got called "Real" because they were not Imaginary. The Real Numbers had no name before Imaginary Numbers were thought of. There can be an infinite number of digits, such as 1 3 = 0.333. Any Number of DigitsĪ Real Number can have any number of digits either side of the decimal point Points to the right are positive, and points to the left are negative.Ī distance is chosen to be "1", then whole numbers are marked off: īut we won't find Infinity, or an Imaginary Number. The Real Number Line is like a geometric line.Ī point is chosen on the line to be the "origin". Mathematicians also play with some special numbers that aren't Real Numbers. Imaginary Numbers like √−1 (the square root of minus 1) Real Numbers can also be positive, negative or zero. Review in Nature (in English, lower half right column of p.Nearly any number you can think of is a Real Number Real Numbers include: He shows that in rational space parts of a figure may disappear by a change of position, that quadratic space is the least space allowing the Euclidean constructions, that transcendental space, though possessing an infinitely greater number of points, does not admit all such constructions. A complex number is a number of the form a + bi, where a and b are real numbers, and i is an indeterminate satisfying i 2 1.For example, 2 + 3i is a complex number.

Now the author considers three kinds of discontinuous space: rational, quadratic and transcendental space, the first containing only points with rational coordinates, the second moreover those whose coordinates imply extractions of square roots, the third only points with transcendental coordinates. Definition An illustration of the complex number z x + iy on the complex plane.The real part is x, and its imaginary part is y. This space consists of all points whose orthogonal rectangular coordinates are algebraic numbers in a given unit of distance. Review in "Revue Semestrielle Des Publications Mathematiques":ĭedekind has defined a discontinuous space in which "so far as he sees" the Euclidean constructions can be made. This appears to the published version of Strong's 1898 Ph.D. Wendell Melville Strong (1871-1942), Is continuity of space necessary to Euclid's geometry (also digitized here), Bulletin of the American Mathematical Society 4 #9 (June 1898), 443-448. Of possible interest is the following paper: That is not what anyone I know means by either "universe" or "exist." Anyway, the answer to this version of the question is that such "universes" "exist," and as I have said people study them in non-standard analysis.
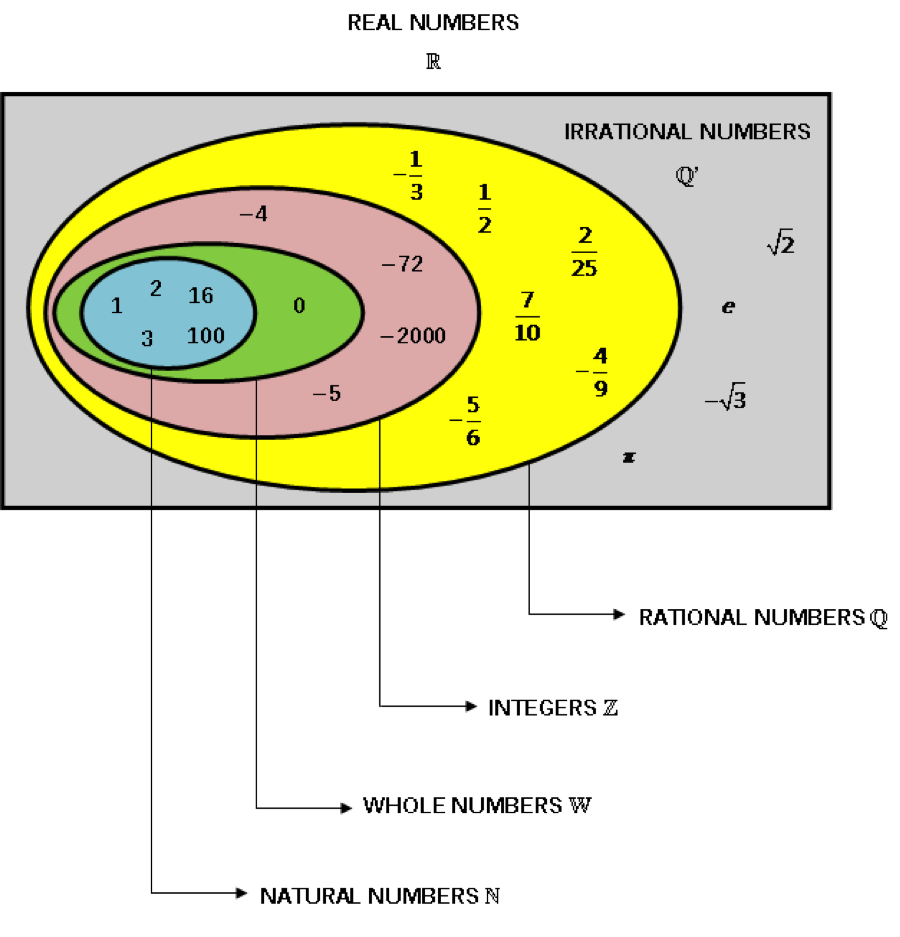
It can be natural numbers, whole numbers, integers, rational numbers, and irrational numbers. There are mathematicians who use extended real number systems for non-standard analysis, but I don't think there are any people who think seriously about using non-standard analysis in physics (although this might change in the future).īy universe I just mean such a thing as Eucildean geometry, and by exist that it is consistent. All the numbers that can be found on a number line. If two possible sets of initial conditions of a system are infinitesimally close, I would expect them to stay infinitesimally close for all time given any reasonable constraints on the system. As any mathematics undergraduate knows, in the hierarchy of number systems that goes N, Z, Q, R, C, (that is, positive integers, integers, rationals, reals. Real numbers are based on the concept on the number. Natural numbers are all numbers 1, 2, 3, 4 They are the numbers you usually count and they will continue on into infinity. This is possible, but what's the point? I can't conceive of a way in which the distinction between two points which are infinitesimally close could matter in, for example, physics, at least in the obvious way. Real numbers are basically all the numbers you could think of if somebody told you to think of a number. Is it possible to have more then a continuum distinct ordered points on a line of length 1? Why do mathematicians mostly use only R for calculus etc, if a number doesnt have to be real? I want to know if what I (or most people) intuitively think of as length of an idealized physical object can be a non-real number. What I'm saying above is that neither of these assumptions is physically realistic beyond a certain precision. Then given any object we can eventually tell what rational lengths are less than its length and what rational lengths are greater than its length, and this gives us a real number by the construction of the real numbers using Dedekind cuts. These ratios are not even numbers! After a certain point, perhaps $10^.


 0 kommentar(er)
0 kommentar(er)
